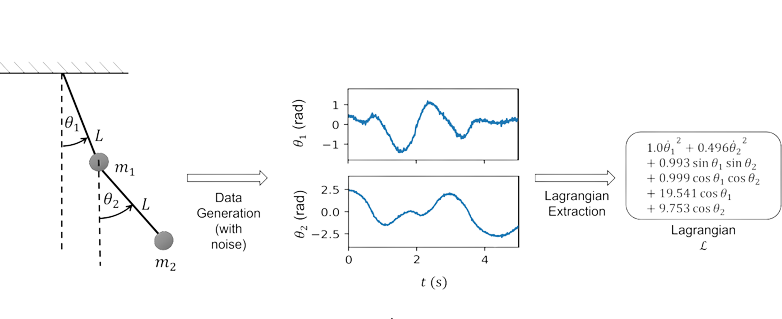
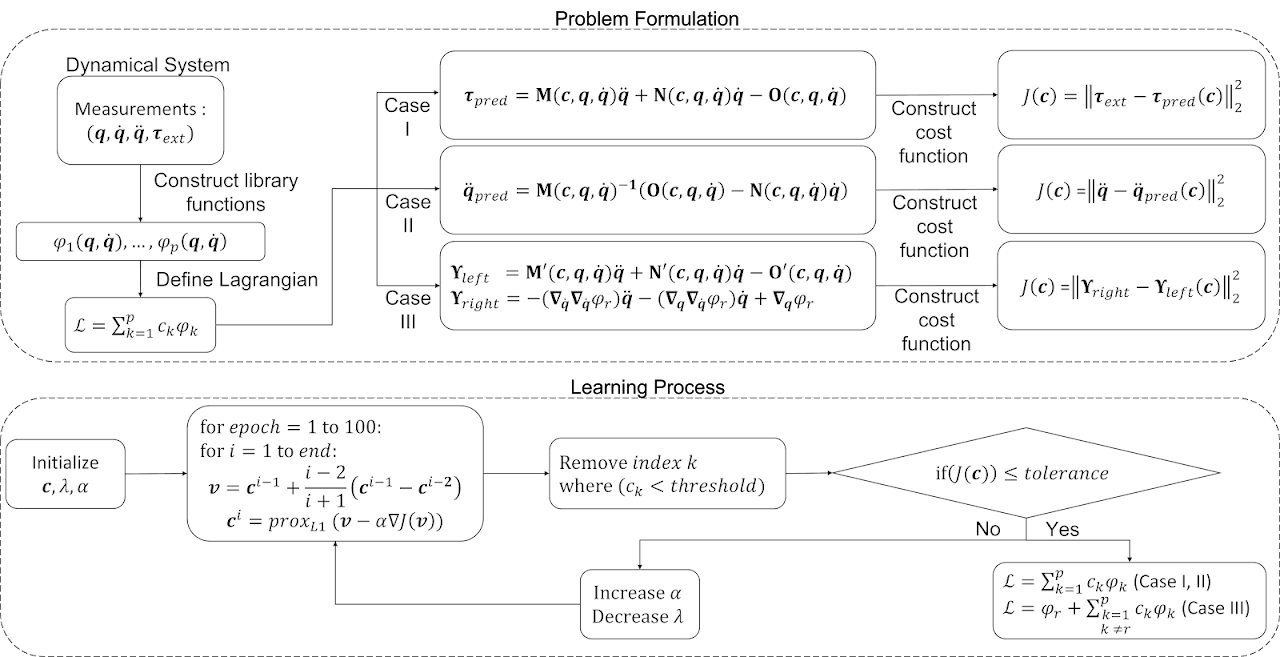
Extended Lagrangian SINDy (xL-SINDy) is a learning-based algorithm designed to obtain the Lagrangian function of nonlinear dynamical systems from noisy measurement data. This method is inspired by SINDy (the Sparse identification of Nonlinear Dynamics) . The Lagrangian function is modeled as a linear combination of nonlinear candidate functions, and Euler-Lagrange’s equation is used to formulate the objective cost function. The optimization of the learning process is done with accelerated proximal gradient descent to obtain a sparse solution. For more detail about the derivation and the problem formulation, please take a look at xL-SINDy xL-SINDy (manuscript in preparation).

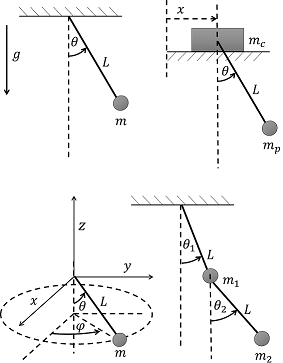
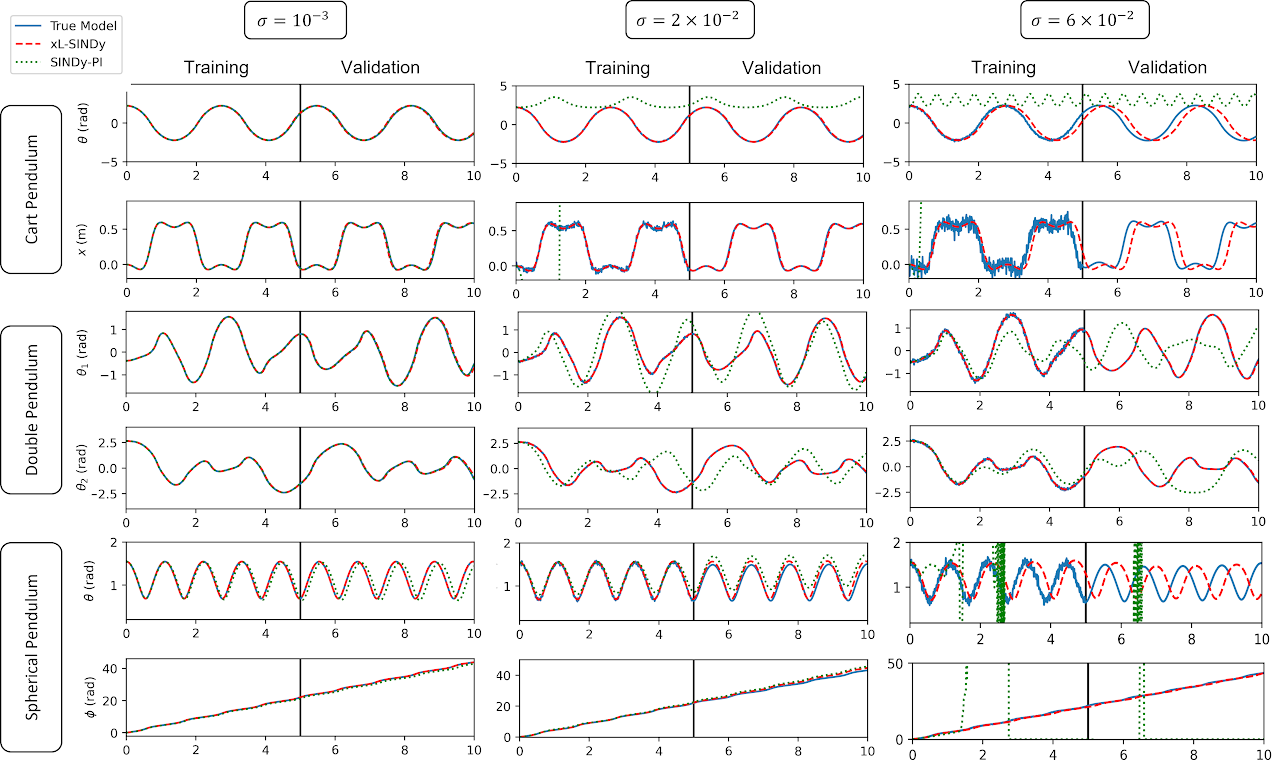
The effectiveness of xL-SINDy is demonstrated against different noise levels in physical simulation with four dynamical systems: A single pendulum, a cart-pendulum, a double pendulum, and a spherical pendulum. The performance of xl-SINDy is also compared to SINDy-PI . Our simulation results demonstrate that xL-SINDy has notably better prediction accuracy compared to SINDy-PI in the presence of higher noise magnitude in all multi-DoF dynamical systems.